Оптимизация измерений NTC-термистора
При изначальном проектировании платы uni_v2 я уделил мало внимания работе с термистором. При программировании, и создании бизнес-логики быстро оказалось, что измерение температуры – это самое популярное применение аналоговым измерениям! Первые опыты также показали, что подход “и так сойдёт” не даёт даже приблизительно точных измерений. Это надо было решать!
В статье немного математических формул о том, как пригодился матан с дифференциальными формулами, которые:
“Никогда нам в жизни не пригодятся!” (c) любой школьник
Я опущу большинство графиков и объяснений – только готовые формулы и результаты для решения моей конкретной задачи.
- Постановка задачки
- I’m afraid, we will have to use MATH
- Что можно было сделать лучше?
- Ответ
- Конвертация измерений микроконтроллера
Постановка задачки
У термистора сопротивление обратно пропорционально температуре. Нам надо подобрать такое пробное сопротивление, чтобы размах напряжений при $T \in [T_{min} .. T_{max}]$ был максимальным для наилучшей точности измерения.
I’m afraid, we will have to use MATH
Взаимосвязь температуры и сопротивления
При $T_0 = 25{}^0C$ у элемента получаем номинальное сопротивление в $R_0 = 10k\Omega$.
! Температура в формулах должна быть в Кельвинах – надо добавлять $273.15K$.
Сопротивление термистора от температуры:
\[R(T) = r_\inf \cdot e^{B / T}\], где:
- $B = 3435K$ – берётся из паспорта изделия
- $r_\inf = R_0 \cdot e^{-\frac{B}{T_0}} = 0.099\Omega$
Отсюда, зависимость температуры от сопротивления:
\[T = \frac{B}{ln(R / r_\inf)}\]Размах делителя напряжения
Банальная схема делителя напряжения: На вход термистора $V_{IN} = 5V$, $Vadc$ должен быть не более $3.3V$.
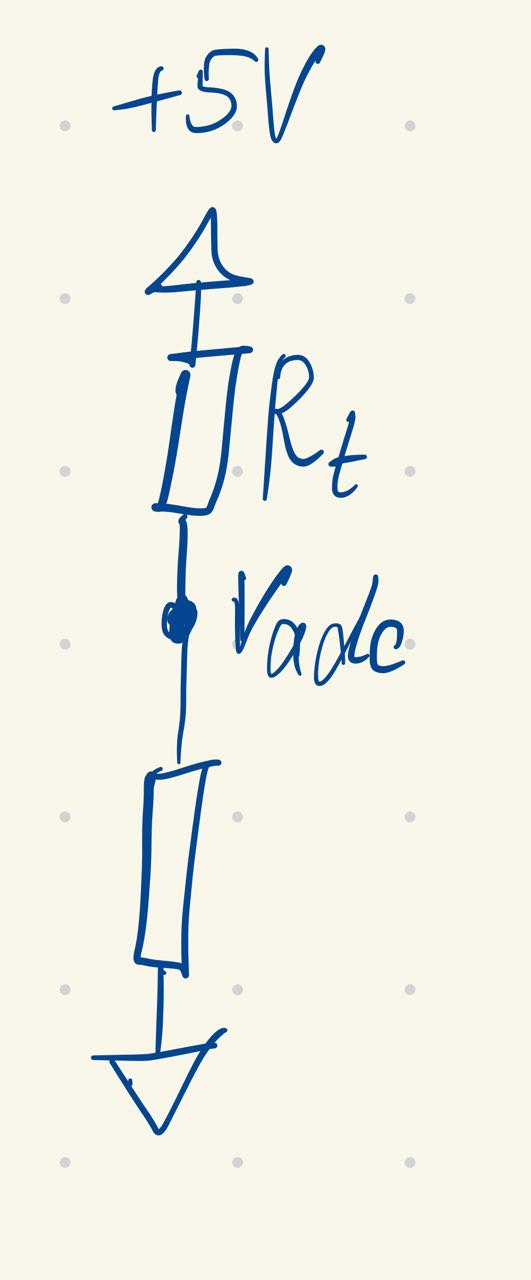
\(Vadc_{max} = V_{IN} \frac{R}{R + R_{min}}\) \(Vadc_{min} = V_{IN} \frac{R}{R + R_{max}}\)
\[\Delta V = V_{IN}R \left( \frac{1}{R + R_{min}} - \frac{1}{R + R_{max}} \right) = \frac{V_{IN} R (R_{max} - R_{min})}{(R + R_{min})\cdot(R + R_{max})}\] \[f = V_{IN}R(R_{max} - R_{min}); g = \frac{1}{R + R_{min}}; j = \frac{1}{R + R_{max}}\] \[\frac {d\Delta V}{dR} = (fgj)' = f'gj + fg'j + fgj' = 0\] \[f' = V_{IN} (R_{max} - R_{min}); g' = -\frac{1}{(R + R_{min})^2}; j' = -\frac{1}{(R + R_{max})^2}\] \[\frac {d\Delta V}{dR} = \frac{\cancel{V_{IN}} \cdot \cancel{(R_{max} - R_{min})}}{(R + R_{min})(R + R_{max})} - \frac{\cancel{V_{IN}} \cdot R \cancel{(R_{max} - R_{min})}}{(R + R_{min})^2(R + R_{max})} - \frac{\cancel{V_{IN}} \cdot R \cancel{(R_{max} - R_{min})}}{(R + R_{min})(R + R_{max})^2}\]\((R + R_{min})(R + R_{max}) - R(R + R_{max}) - R(R + R_{min}) = 0 \rightarrow -R^2 + R_{min}R_{max} = 0\) \(R^2 = R_{min}R_{max} \rightarrow \mathbf{R_{optimal} = \sqrt{R_{min}R_{max}}}\)
Таким образом, для оптимального измерения температур в диапазоне $ T \in [-10^0C .. +100^0C] $ нам нужен делитель, общим сопротивлением $6.745k\Omega$.
Используя ряд номиналов E24, находим самую близкую комбинацию, которая даёт нам деление $\frac{3.3}{5.0} = 0.(6)$ с заданным суммарным сопротивлением – это $4.8k\Omega$ + $2.4k\Omega$.
Пользуясь формулами, мы теперь можем построить графики для оценки зависимости точности измерения температуры от текущей температуры.
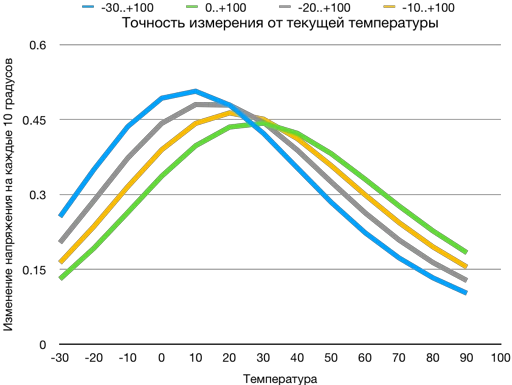
Нас интересует получениие наибольшей точности в районе $20..25^0C$ – для этого я и выбрал диапазон измерения температур $[-10..+100]^0C$. С учётом выбранного выше делителя $4.8k\Omega$ + $2.4k\Omega$ я могу измерять любые температуры, которые может выдержать датчик. Я лишь потеряю в точности.
Что можно было сделать лучше?
Правильнее было бы оттолкнуться от сопротивления делителя, и избежать всей этой дифференциальщины. Выбрать делитель, с которым у меня была бы наилучшая точность в интересующем диапазоне температур. И, затем, чуть его поправить, чтобы предельные температуры не сожгли случайно аналоговую схему.
Ответ
Для NTC-термистора с параметром $B = 3435K$ и наибольшей точностью в диапазоне температур $T \in [20..25]^0C$ мы должны выбрать делитель $4.8k\Omega$ + $2.4k\Omega$.
Конвертация измерений микроконтроллера
Микроконтроллер возвращает целое число $ADC$ в диапазоне $ADC \in [0..4095]$. В напряжение переводим по формуле:
\[u(ADC) = V_{dda} \cdot \frac{ADC}{4095}\], где:
- $V_{dda} – напряжение питания микроконтроллера, которое мы измеряем его внутренним функционалом, завязанным на калиброванный внутренний источник напряжения.
Измеренное напряжение – это напряжение выхода Операционного Усилителя (ОУ). Оно с обратной связью и делителем.
Может, позже добавлю электрическую схему для полного понимания.
Делитель “верхний”, который на обратной связи ОУ – его соотношение равно $b$. А соотношение делителя входного, “нижнего”, который мы вычисляли на протяжении всей этой статьи, – это $a$.
Отсюда, напряжение на входе в “нижний” делитель: $V = u(ADC) \frac{1-b}{a}$.
Немного пожонглировав, получаем формулу для нахождения температуры из измеренного напряжения:
\[T = B / ln \left\{ \frac{R}{r_\inf} \left( \frac{V_{IN} \cdot a}{u(1-b)+V_{vdda}b} - 1 \right) \right\}\]